|
In
Their Own Words
 n
Wilbur's time, the "angle of incidence" was what we now call the "angle
of attack" -- the angle at which the wing of an airplane meets the wind.
This is difficult to measure in the field with any accuracy, so Wilbur
suggests that it might be measured indirectly by using three
variables that can be more easily determined, then using a chart to look up
the angle. Besides the subject at hand, this article reveals three
things concerning Wilbur's character, his focus, and his methods. First
it shows that Wilbur, although he is a newcomer to field of aeronautics,
has the self-confidence to challenge other, more experienced scientists.
Second, the movements he describes are the sorts that an unpowered
glider would make -- Wilbur is focused on soaring flight. And
finally, he paints a series of triangles and angles to make his
analysis. Wilbur is using trigonometry to analyze the phenomenon of
flight. It has been said that the invention of the airplane was a
triumph of trigonometry, and this is the first battle fought and won.
If the term “angle of incidence," so frequently
used in aeronautical discussions, could be confined to a single definite
meaning, viz., the angle at which aeroplane and wind actually meet, much
error and confusion would be averted. But many of the best writers use
this term loosely and inexactly, with the result that- their
calculations and explanations of phenomena are thereby often rendered of
little value, and students are misled.
If a plane be held stationary in a horizontal wind (Fig. I), the
angle of incidence A C D will be equal to the angle with the horizon.
But if the wind has an upward trend, the angle of incidence will be
increased to A C D2. A calculation based on the assumption that A C D
still remained the true angle would, of course, be seriously in error.
If it be assumed (Fig. 2) that the wind moves from D to C, while
the plane moves from D2 to C, the angle of incidence will become A C D3.
The wind having an apparent horizontal speed of F C + E C, which is
equal to F2C as compared with a vertical speed of D2F, the wind will
appear to strike the plane from the direction D3C, thus making its angle
of incidence A C D3 instead of A C D2. Taking still another case (Fig.
3), in which the wind moves from D2 to C, while the plane is rising from
C to C2 the angle of incidence will be A C X. The horizontal speed of
the wind will be F C. and its apparent vertical speed D2 F - C C2 = X F,
so that the wind will appear to strike the plane from the direction X C.
If the plane had fallen from C to C3 the angle of incidence would have
been A C X2, since the vertical motion would now have been D3 F + C C3 = X2
F. A study of the foregoing will lead to the conclusion that in order to
obtain the angle of incidence it is first necessary to know correctly
(1) the angle of the plane with the horizon; (2) the horizontal speed of
the wind; (3) the vertical speed of the wind; (4) the horizontal speed
of the plane; (5) the vertical spend of the plane. Now, since the
probability of obtaining five correct simultaneous measurements is very
slight when the observation is taken in the open air and since the
soaring angle is not. supposed to exceed three degrees, it is evident
that calculations based upon observations of soaring birds are of
exceedingly doubtful value.
But though direct attempts to calculate the angle of incidence
promise little for accuracy, another method remains by which
approximately correct results may be obtained. The tables of Langley,
Lilionthal, Chanutc, and others give with a good degree of accuracy, the
vertical component of the normal pressure at all angles and speeds, both
for planes and curved surfaces. Now, since the elements of these tables
are four, viz., area, speed, angle, and lift, it follows that three
factors being known the fourth may readily be obtained. The angle of
incidence may be calculated in any case where speed, lift, and area are
commensurable. Of these, area may be obtained by actual measurement.
Lift is equal to weight supported, and can also be exactly measured.
Speed alone requires to be calculated at the instant the observation is
made. Thus the opportunity for error is reduced to a single item, and
this the one which affects the result least seriously in case of a
slight error. It is easier to measure speeds than angles and errors are
less costly. There is, of course, a possibility of error in the tables,
but the results have been confirmed by the experiments of independent
observers, and are believed to be substantially correct. Calculations of
the angle of incidence based upon this plan would scarcely be so
seriously in error as that of a well-known writer based upon
observations of soaring gulls, in which he obtained from his
measurements of angles and speeds an angle of incidence which called for
an upward lift of nearly three pounds upon a two-pound bird. It was his
idea that the excess of lift was expended in raising the bird above its
original level. This, however, is scarcely a satisfactory explanation of
how a lift of three pounds could be applied to a two-pound bird in
contradiction of the law that action and reaction are always equal. It
would lie more reasonable to assume that the excessive lift never
existed, but that the upward motion of the bird kept the angle of
incidence (Fig. 3) reduced to a point where the lift was just equal to
the bird's weight, all of the time.
If students of aeronautical problems will constantly bear in mind
that (1) area of surface; (2) weight or lift; (3) relative speed are the
only factors concerned in determining the angle of incidence, many
errors will be detected and much trouble saved. It is clear that a bird,
instead of possessing flull control of its angle of incidence (as
writers sometimes assume), is, in fact, almost powerless to change it.
The bird is really itself controlled by a kind of automatic governor,
for a gust of wind which tends to increase the lift; is balked by the
Fact that the weight of the bird is not sufficient to furnish the
required reaction, and the bird must either float back horizontally with
a speed equal to the increase in the velocity of the wind, or it will
involuntarily be raised at a speed sufficient to keep its angle of
incidence at a point where the increased lifting pressure naturally due
to the increased speed will be exactly counterbalanced. Nevertheless the
bird can, to a limited extent, affect its area, its weight, and its
speed, and thus indirectly its angle of incidence also. Its area may be
reduced (and its angle increased) by partly folding its wings, but as,
in actual practice, a folding of the wings always accompanies an
increase of relative velocity (which produces a decrease in angle), the
real effect is to preserve the original angle instead of changing it.
The apparent weight may be momentarily increased by a sudden curve in
the direction of motion, in which case the momentum of its body acts to
produce a centrifugal force which increases the downward pressure on its
wings, and this requires an increase in the angle of incidence to
furnish the required extra support. Speed may be controlled by
increasing or decreasing the elevation of the bird or its rate of fall.
But. none of these changes in speed, area or weight, quickly and
permanently affect its angle of incidence; The bird can at will vary its
angle with the horizon, even to the extent of three hundred and sixty
degrees in loss than a second, as when it turns a complete somersault in
the air: but its angle of incidence probably does not vary as much as
one-twentieth of that amount in the same case. It is very important to
distinguish carefully between the angle of incidence, and the angle with
the horizon, as the latter has nothing at all per se to do with the
former. By keeping the distinction, carefully in mind, the student will
quickly obtain new ideas of the correct explanation of the action of the
Penaud tail used by Lilienthal, Pilcher, and Chanute; and correct the
sequence of cause and effect in many explanations of phenomena which
occur in aeronautical writings.
Since the formulation of a principle into a rule often serves to fix
it more prominently in the mind, the writer ventures to offer the
following:
Rule.—The angle of incidence is fixed by area, weight, and speed
alone. It varies directly as the weight, and inversely as the area
and speed, though not in exact ratio.
|
The cover of the Aeronautical Journal from July 1901. Wilbur's article
began on page 47.
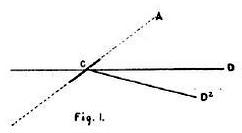
Figure 1
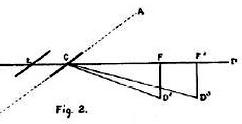
Figure 2
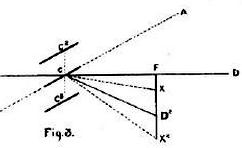
Figure 3
|
The Angle of 
Need
to 
